Close nucleon encounters

Scientists believe that the crushing forces in the core of neutron stars squeeze nucleons so tightly that they may blur together. Recently, an experiment by Kim Egiyan and colleagues in Hall B at the US Department of Energy’s Jefferson Lab (JLab) caught a glimpse of this extreme environment in ordinary matter here on Earth. Using the CEBAF Large Acceptance Spectrometer (CLAS), the team measured ratios of the cross-sections for electrons scattering with large momentum transfer off medium and light nuclei in the kinematic region that is forbidden for scattering off low momentum nucleons. Steps in the value of this ratio appear to be the first direct observation of the short-range correlations (SRCs) of two and three nucleons in nuclei, with local densities comparable to those in the cores of neutron stars.

SRCs are intimately connected to the fundamental issue of why nuclei are dilute bound systems of nucleons. The long-range attraction between nucleons would lead to a collapse of a heavy nucleus into an object the size of a hadron if there were no short-range repulsion. Including a repulsive interaction at distances where nucleons come close together, ≤0.7 fm, leads to a reasonable prediction of the present description of the low-energy properties of nuclei, such as binding energy and saturation of nuclear densities. The price is the prediction of significant SRCs in nuclei.

For many decades, directly observing SRCs was considered an important, though elusive, task of nuclear physics; the advent of high-energy electron-nucleus scattering appears to have changed all this. The reason is similar to the situation encountered in particle physics: though the quark structure of hadrons was conjectured in the mid-1960s, it took deep inelastic scattering experiments at SLAC and elsewhere in the mid-1970s to prove directly the presence of quarks. Similarly, to resolve SRCs, one needs to transfer to the nucleus energy and momentum >=1 GeV, which is much larger than the characteristic energies/momenta involved in the short-distance nucleon-nucleon interaction. At these higher momentum transfers, one can test two fundamental features of SRCs: first, that the shape of the high-momentum component (>300 MeV/c) of the wave function is independent of the nuclear environment, and second, the balancing of a high-momentum nucleon by, predominantly, just one nucleon and not by the nucleus as a whole.

The inclusive nature of the process ensures that the final-state interaction does not modify the ratios of the cross-sections

An extra trick required is to select kinematics where scattering off low momentum nucleons is strongly suppressed. This is pretty straightforward at high energies. First, one needs to select kinematics sufficiently far from the regions allowed for scattering off a free nucleon, i.e. x = Q²/2q₀m_N < 1, and for the scattering off two nucleons with overall small momentum in the nucleus, x < 2. (Here Q² is the square of the four momenta transferred to the nucleus, and q₀ is the energy transferred to the nucleus.) In addition, one needs to restrict Q² to values of less than a few giga-electron-volts squared; in this case, nucleons can be treated as partons with structure, since the nucleon remains intact in the final state due to final phase-volume restrictions.

If the virtual photon scatters off a two-nucleon SRC at x > 1, the process goes as follows in the target rest frame. First, the photon is absorbed by a nucleon in the SRC with momentum opposite to that of the photon; this nucleon is turned around and two nucleons then fly out of the nucleus in the forward direction. The inclusive nature of the process ensures that the final-state interaction does not modify the ratios of the cross-sections. Accordingly, in the region where scattering off two-nucleon SRCs dominates (which for Q² ≥ 1.4 GeV² corresponds to x > 1.5), one predicts that the ratio of the cross-section for scattering off a nucleus to that off a deuteron should exhibit scaling, namely it should be constant independent of x and Q² (Frankfurt and Strikman 1981). In the 1980s, data were collected at SLAC for x > 1. However, they were in somewhat different kinematic regions for the lightest and heavier nuclei. Only in 1993 did the sustained efforts of Donal Day and collaborators to interpolate these data to the same kinematics lead to the first evidence for scaling, but the accuracy was not very high.

An experiment with the CLAS detector at JLab was the first to take data on 3He and several heavier nuclei, up to iron, with identical kinematics, and the collaboration reported their first findings in 2003 (Egiyan et al. 2003). Using the 4.5 GeV continuous electron beam available at the lab’s Continuous Electron Beam Accelerator Facility (CEBAF), they found the expected scaling behaviour for the cross-section ratios at 1.5 ≤ x ≤ 2 with high precision.

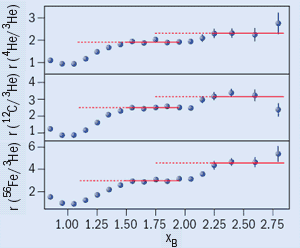
The next step was to look for the even more elusive SRC of three nucleons. It is practically impossible to observe such correlations in intermediate energy processes. However, at high Q2, it is straightforward to suppress scattering off both slow nucleons and two-nucleon SRCs. One needs only to reach the x ≥ 2 region where scattering off a deuteron is kinematically forbidden. Here, the experiment typically probes scattering off a fast nucleon with momentum opposite to the virtual photon, with two nucleons balancing the fast nucleon’s momentum.

Again, a scaling of the ratios was expected. In this case, however, the ratios of the cross-sections for a pair of nuclei of masses A1 and A2 and with A₁ > A₂ was predicted to be higher for 2 ≤ x ≤ 3 than for 1.5 ≤ x ≤ 2. This is because there is a high probability for a nucleon to have two nearby nucleons in a heavier, denser nucleus. Hence, one expected to find two steps. This is exactly what the CLAS experiment observed in data recently reported for these kinematics and shown in figure 3 (Egiyan et al. 2005). Moreover, the iron:carbon ratios for x ˜ 1.7 and 2.5 are consistent with the expectation that the probability of two- and three-nucleon SRCs should increase with A as the square and cube, respectively, of the nuclear density. For iron, the probability of two-nucleon SRCs reaches about 25%.

More data for exploring SRCs have already been taken at JLab, and several more efforts are already planned to study this interesting region of nuclear physics, which has important implications for the dynamics of the cores of neutron stars.